背景

在20世纪早期，通信技术的迅猛发展引起了人们对信息传递和处理的关注。在过去，人们主要集中于电信号的传输和解调技术，但在实际通信中，信号的传输可能受到噪声和失真的干扰，导致信息的丢失或错误。

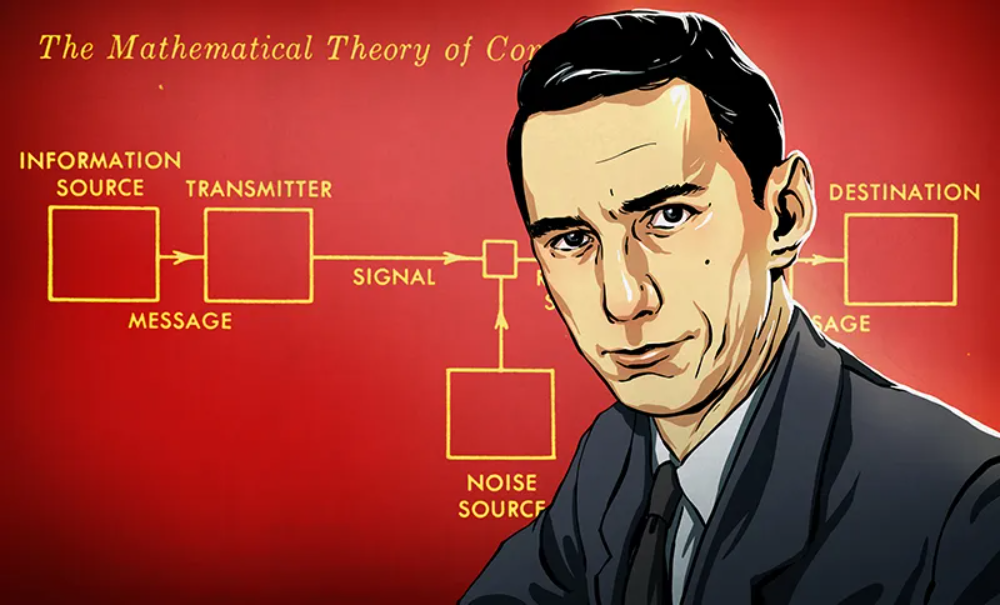
1948年，克劳德·香农发表了一篇名为《通信的数学理论》（A Mathematical Theory of Communication）的里程碑性论文，该论文奠定了信息论的基础。香农的论文提出了一种全新的方法，将信息从直觉和语义层面抽象为数学模型，从而使信息的传输、编码、压缩等问题可以用精确的数学语言来描述和解决。

克劳德·香农（1916年-2001年）是美国电气工程师、数学家和密码学家。他生于密歇根州，曾就读于麻省理工学院，并在贝尔实验室（Bell Labs）工作。他被誉为“信息论之父”，因为他的论文《通信的数学理论》在信息论的发展和应用中起到了划时代的作用。香农的《通信的数学理论》不仅仅是一篇研究论文，而是一种全新的思维方式。他引入了信息熵的概念，这是信息论中最著名和核心的概念之一，用于度量信息的不确定性。他还提出了香农熵（Shannon entropy）的计算方法，这成为了信息熵的标准计算方式。

概念

信息熵是信息论中的一个重要概念，用于衡量随机变量中的不确定性或信息量。它最初由香农（Claude Shannon）在1948年提出，是信息论的核心概念之一。

在信息论中，信息熵是对一系列消息或事件发生概率的度量。高概率事件携带较少信息，因为它们较为预测和常见；而低概率事件携带较多信息，因为它们较为罕见和意外。比如，某市发生了一件凶杀案，警察对案发现场进行了调查后锁定了3个嫌疑人。而对他们审问后得到的信息均是警察已经获知的确定性内容（高概率事件），所以信息量少。如果有人提供了警察尚未掌握的关键情报（低概率事件），那么信息量也就大。

信息熵可以用来衡量信息源的平均不确定性，或者说信息源中所包含的平均信息量。当一个信息源的信息熵最大时，意味着它具有最大的不确定性，其中的每个事件概率相等，信息最丰富。相反，当信息熵为0时，信息源是确定性的，每个事件概率都为1，不包含任何信息。

定义

信息熵的数学定义

对于一个离散随机变量$X$，其信息熵$H(X)$定义为： $$ H(X) = -\sum_{x \in X} p(x) \log_2(p(x)) $$ 其中，$P(x)$是随机变量$X$取值为$x$的概率，$\sum$表示对所有可能的取值$x$求和，$\log_2$表示以$2$为底的对数。信息熵的单位通常以比特（bit）为基础.

计算

eg1:

一个只有正反面的硬币随机扔一次的事件 $$ H(X)=-2 \times \frac{1}{2} \log_2\left(\frac{1}{2}\right) = 1 $$ eg2:

从一盒扑克牌中随机抽出一张扑克的种类 $$ H(X)=-4 \times \frac{1}{4} \log_2\left(\frac{1}{4}\right) = 2 $$ eg3:

从一个八等分的旋转轮盘旋转一次的结果 $$ H(X)=-8 \times \frac{1}{8} \log_2\left(\frac{1}{8}\right) = 3 $$ eg4:

随机扔一次骰子的结果 $$ H(X)=-6 \times \frac{1}{6} \log_2\left(\frac{1}{6}\right) = 2.58 $$