*eg.*以3个一维简谐振子组成的独立的定域子体系为例,体系的总能量$U = \frac{9}{2}h\nu$,体系的体积为$V$,这时体系的宏观态可通过状态参量表示为$(\frac{9}{2}h\nu,V,3)$.有多少种可能的排布方式?
树是一种数据结构,它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
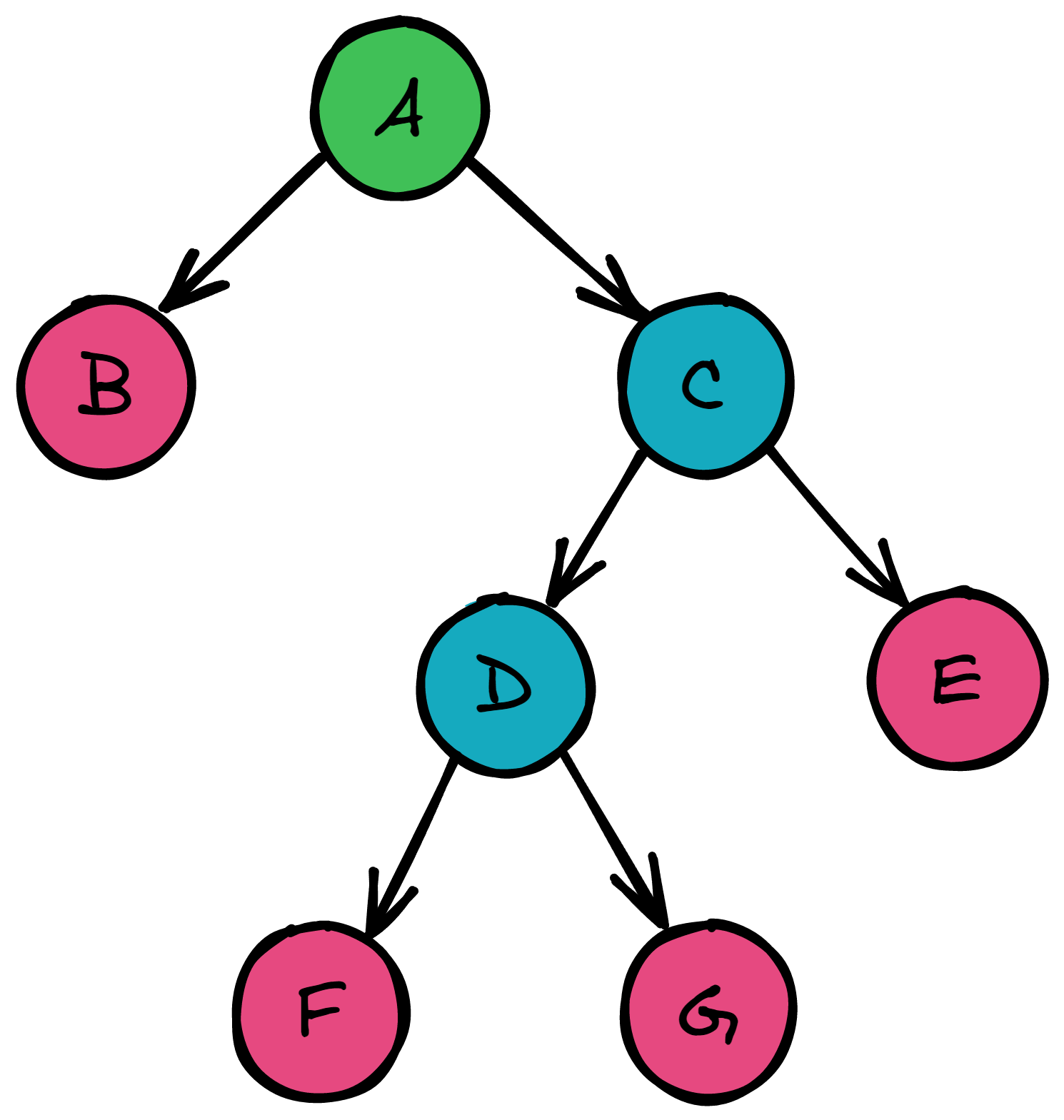
有3个一维简谐振子,即让3个粒子依次分配在能级上。而总能量$U=\frac{9}{2}h\nu$,所以一个粒子的最高处于$E_3=\frac{7}{2}h\nu$上。
从数学上,我们可以通过3层分类讨论实现枚举可能的分布方式,即先枚举第一个粒子的能级,然后枚举第二个粒子的能级,最后枚举第三个粒子的能级。
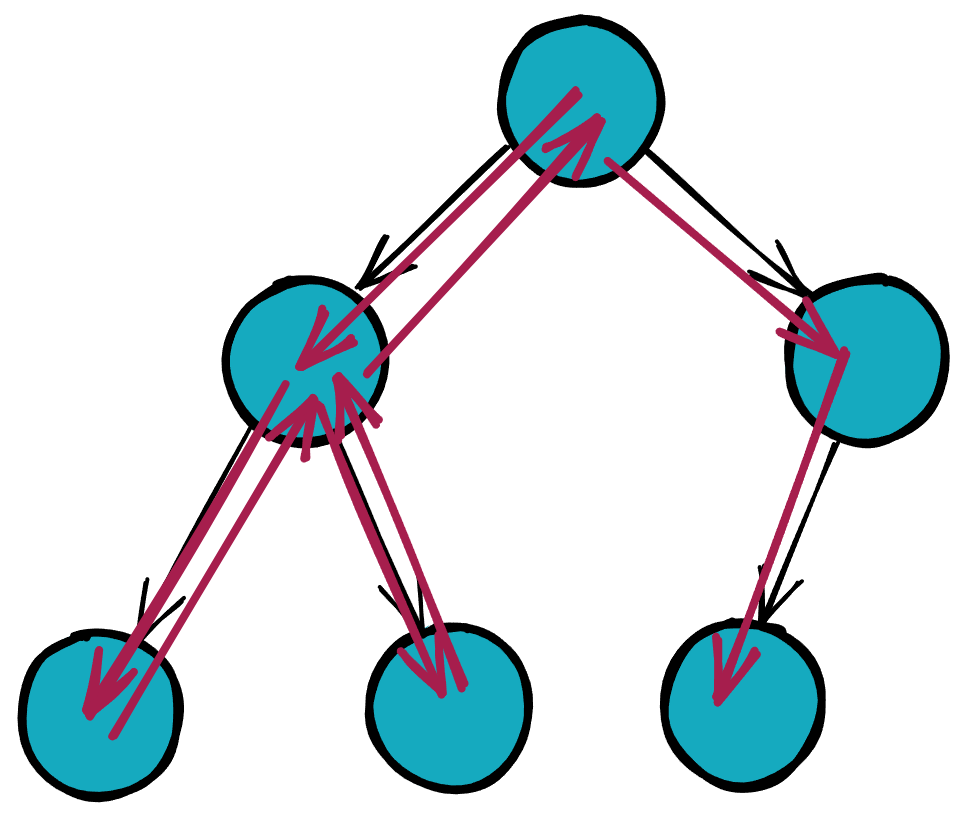
其枚举路线图实际上是一种树型结构,如图所示。紫色代表合法的排布方式枚举出口,红色代表已经不合法的排布方式,所以没有必要继续枚举了。

那么如何去遍历这棵树呢?这里可以考虑最常见的搜索算法-深度优先搜索算法(DFS)。同时,用递归函数去具体实现。
深度优先搜索算法(Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索树的分支。
递归函数是一种具体的编程代码实现方式。编程语言中,函数直接或间接调用函数本身,则该函数称为递归函数。可以类比数列的递推关系式,如下数列的Python递归函数代码实现。
$$
a_n=
\begin{cases}
0&,n=1
\
a_{n-1}+1&,n>1
\end{cases}
$$
1
2
3
4
|
def a(n):
if n <= 1:
return 0
return a(n-1)+1
|
即上述问题的Python代码实现为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
N = 3 # 粒子数目
E = 9/2 # 体系能量
A = []
T = [0]*N
m = int(E-N+1)+1
D = dict()
def f(v):
return v+1/2
def dfs(x):
if sum(T) > E:
return
if x == N:
if sum([f(i) for i in T]) == E:
d = getDist(T)
if d in D:
D[d] += 1
else:
D[d] = 1
A.append(T.copy())
return
for i in range(m+1):
T[x] = i
dfs(x+1)
T[x] = 0
def getDist(t):
lst = [0]*(m+1)
for i in t:
lst[i] += 1
return "-".join([str(i) for i in lst])
dfs(0)
with open('answer.txt','w') as f:
f.write("体系各种可能的能级分布为:\n")
f.write("|能级\t|")
dn = len(D)
for i in range(dn):
f.write("分布类型%d\t|"%(i+1))
f.write('\n')
DT = [x.split('-') for x in list(D.keys())]
DT = [[int(i) for i in X] for X in DT]
TB = [[0 for i in range(dn)] for j in range(m+1)]
for i in range(m+1):
for j in range(dn):
TB[i][j] = int(DT[j][i])
for i in range(m+1):
f.write("|%d/2hv\t|"%(2*i+1))
for j in range(dn):
f.write("%d\t|"%TB[i][j])
f.write('\n')
NM = list(D.values())
f.write('|\t|')
for i in range(dn):
f.write("%d\t|"%NM[i])
f.write('\n')
O = sum(D.values())
G = max(D.values())
f.write("Ω=%d\n"%O)
f.write("最概然分布出现的数学概率为%d/%d=%d%%"%(G,O,int(G/O*100)))
|
输出结果
体系各种可能的能级分布为:
| 能级 |
分布类型1 |
分布类型2 |
分布类型3 |
| 1/2hv |
2 |
1 |
0 |
| 3/2hv |
0 |
1 |
3 |
| 5/2hv |
0 |
1 |
0 |
| 7/2hv |
1 |
0 |
0 |
|
3 |
6 |
1 |
Ω=10
最概然分布出现的数学概率为6/10=60%

