题目

3181. 执行操作可获得的最大总奖励 II 困难

给你一个整数数组 rewardValues，长度为 n，代表奖励的值。

最初，你的总奖励 x 为 0，所有下标都是 未标记 的。你可以执行以下操作 任意次 ：

• 从区间 [0, n - 1] 中选择一个 未标记 的下标 i。
• 如果 rewardValues[i] 大于 你当前的总奖励 x，则将 rewardValues[i] 加到 x 上（即 x = x + rewardValues[i]），并 标记 下标 i。

以整数形式返回执行最优操作能够获得的 最大 总奖励。

示例 1：

输入： rewardValues = [1,1,3,3]

输出： 4

解释：

依次标记下标 0 和 2，总奖励为 4，这是可获得的最大值。

示例 2：

输入： rewardValues = [1,6,4,3,2]

输出： 11

解释：

依次标记下标 0、2 和 1。总奖励为 11，这是可获得的最大值。

提示：

• 1 <= rewardValues.length <= 5 * 10^4
• 1 <= rewardValues[i] <= 5 * 10^4

题解

由题意可知，每个相同的值最多被标记一次，同时要奖励最大化。这其实就是01背包问题，但是数据有些大，需要做一些特殊的优化处理。

在数据范围不大的情况下（3180. 执行操作可获得的最大总奖励 I），我们可以定义 f[i][j] 表示能否从前 i 个数中得到总奖励 j，即一个布尔dp数组。

考虑v=rewardValues[i]选或不选：

不选 v：$f[i][j]=f[i−1][j]$ 选 v：$f[i][j]=f[i−1][j−v]$，前提是 $j \geq v$ 且 $j−v<v$，即 $v \leq j < 2v$。

满足其一即可，得 $$ f[i][j]=f[i−1][j]∨f[i−1][j−v] $$ 其中 ∨ 即编程语言中的 ||。

初始值 f[0][0]=true。

答案为最大的满足 f[n][j]=true 的 j。

但在目前的数据范围下，显然二维dp是存不下的，这里可以使用一个bigint或bitset优化数组。使用Python的话int本身就可以为bigint，这样代码也会简洁很多。

这里使用一个二进制整数f表示当前有哪些总奖励是可以达到的，每个二进制的位数就是原来的dp[i][j]的j，如果二进制某一位数是1就代表可以达到这个总奖励。

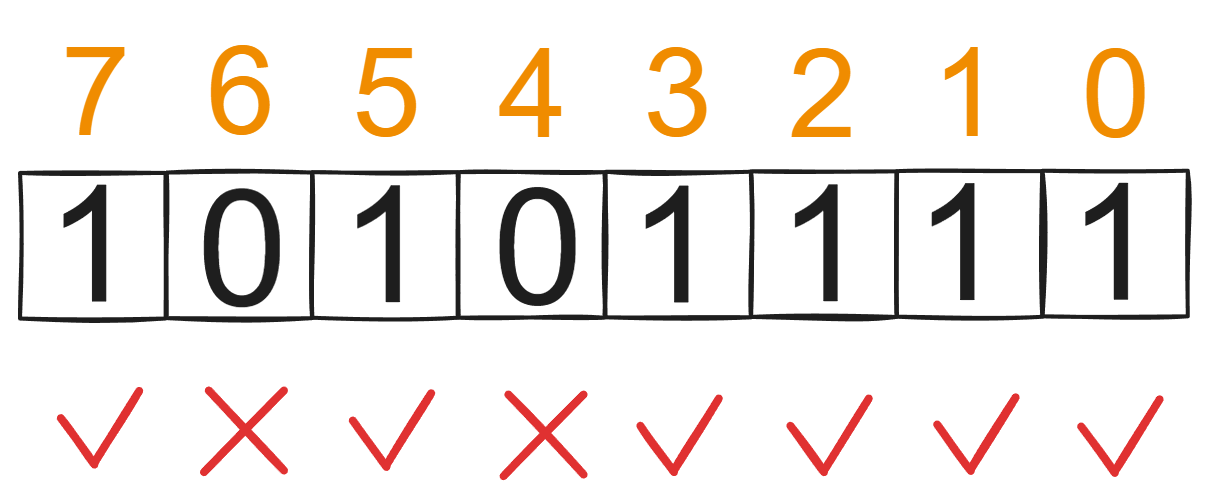
如上面的二进制数代表总奖励为0,1,2,3,5,7是可以达到的，所以最大的总奖励就是7.

那么如何更新这个二进制f数组，就需要巧妙的应用二进制的左移<<、逻辑与&&、逻辑或||。

在那之前首先要做排序和去重。之前二维f[i][j]的逻辑或操作，在二进制中使用逻辑或||就可以快64倍（一般编程语言中的整数最大是int64，其中bigint和bitset的实现原理应该也之基于int64）。

初始的f=1代表总奖励为0是可以达到的。

假设rewardValues = [1,1,3,3],去重排序后rewardValues = [1,3]。

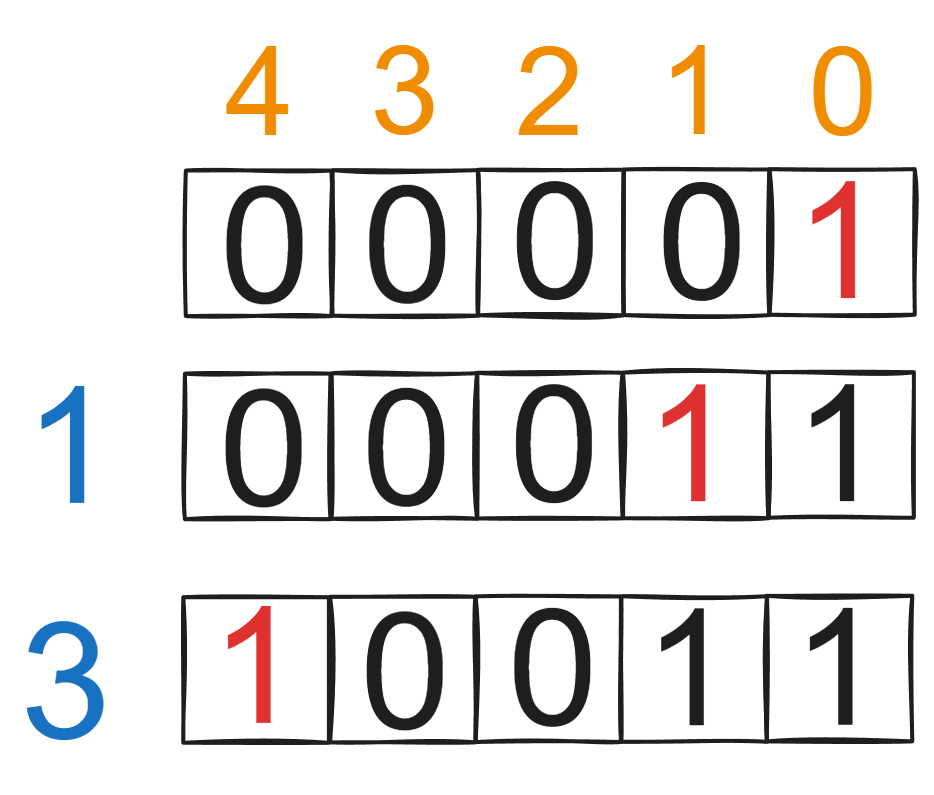
如上图所示遍历数组rewardValues，然后一步一步更新最新可以到达的总奖励数。

下一个状态的f应该继承所有前一个状态的f可以到达的总奖励，即使用逻辑或。 $$ f_{new} = f_{old} \or f’ $$

• $f_{new}$ 是新的状态值
• $f_{old}$ 是上个奖励的状态值
• $f’$ 是这次奖励后的增量状态值

如果要在旧的奖励数上添加当前奖励，那么可以使用二进制的左移运算，例如当前奖励是v $$ f’ = f_{old} « v $$ 但是选择该奖励的前提是他没有超过原来总奖励，那要怎么保证呢？

假设rewardValues = [2,3,4]，如图所示。

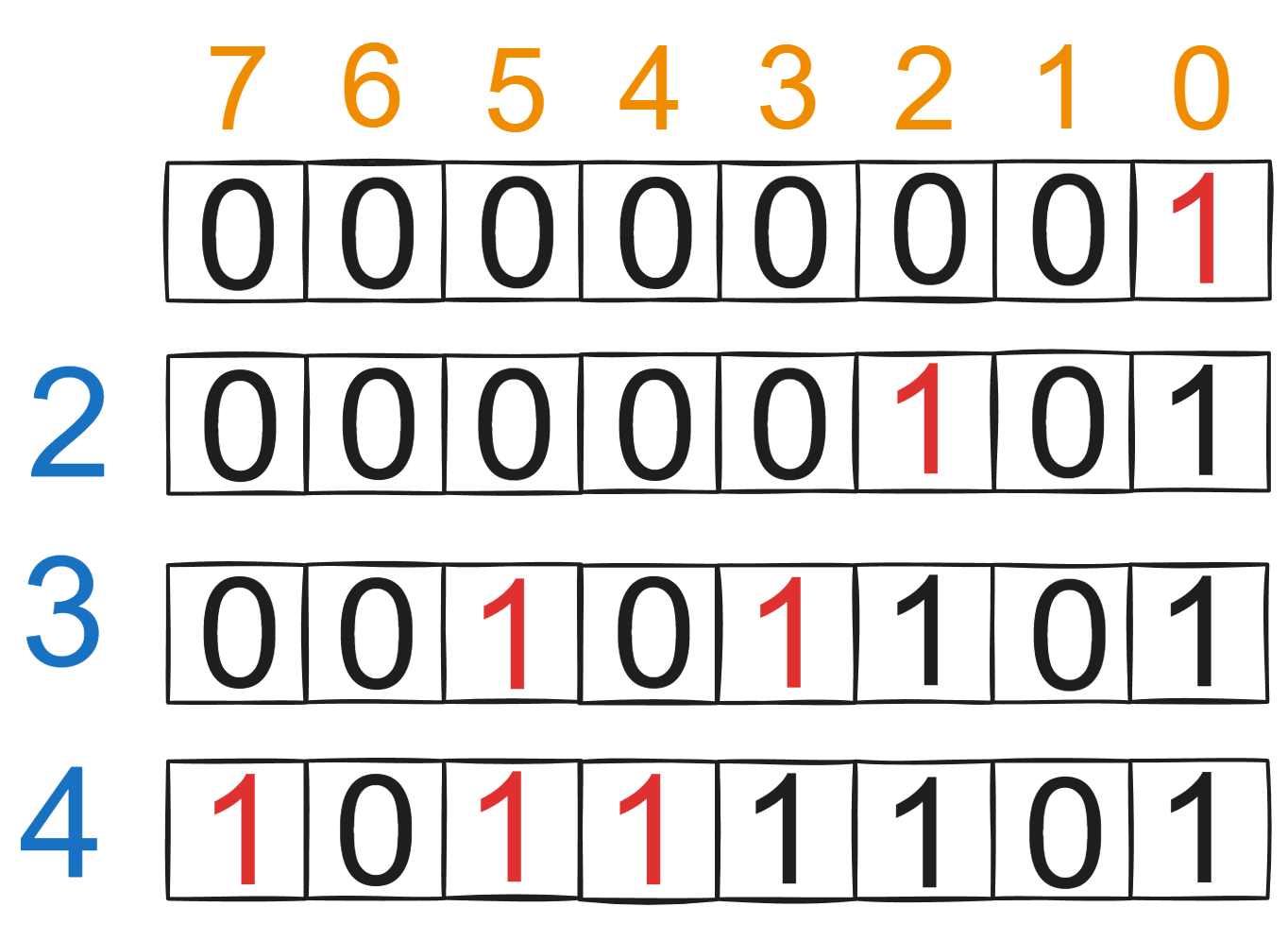
没有办法同时选择标记[2,3,4]，最大值应该是7，即标记了3,4.

在更新奖励4的时候应该把之前总奖励小于4的值保留，大于等于的值全部置零，代表这些为1的数字可以左移继续标记选择4. 在数学中我们可以使用逻辑与的方式实现过滤掉超过的值。一个总奖励小于4的二进制状态f可以通过如下方式获得： $$ f’’ = f_{old} \and ((1«4)-1) $$

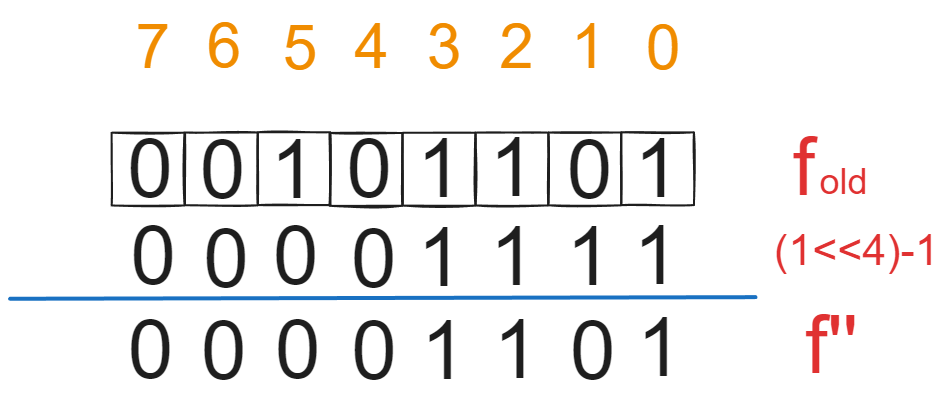
然后这些被过滤后的状态值f''都都小于当前奖励可以选择，再做左移操作就能得到增量状态值f'。 $$ f’=f’’«v=(f_{old} \and ((1«v)-1)) « v $$ 综上可得f的迭代关系式为： $$ f_{new} = f_{old} \or ((f_{old} \and ((1«v)-1)) « v) $$ 最终的答案就是f二进制的最高位1的位数-1.

代码

1
2
3
4
5
6
7
8

class Solution:
    def maxTotalReward(self, rewardValues: List[int]) -> int:
        rewardValues = list(set(rewardValues))
        rewardValues.sort()
        f = 1
        for v in rewardValues:
            f |= (f&((1<<v)-1))<<v
        return f.bit_length()-1

还可以进一步优化：

1. 设 m=max(rewardValues)，如果数组中包含 m−1，则答案为 2m−1（因为这是答案的上界），无需计算 DP。

2. 如果有两个不同元素之和等于 m−1，也可以直接返回 2m−1。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution:
    def maxTotalReward(self, rewardValues: List[int]) -> int:
        m = max(rewardValues)
        s = set()
        for v in rewardValues:
            if v in s:
                continue
            if v == m - 1 or m - 1 - v in s:
                return m * 2 - 1
            s.add(v)

        f = 1
        for v in sorted(s):
            f |= (f & ((1 << v) - 1)) << v
        return f.bit_length() - 1